Алгоритмы
- Selection sort
- Insertion sort
- Shellsort
- Heap Sort
- Counting Sort
- Одновременный поиск минимума и максимума в массиве
- Хэш-таблица с открытой адресацией
- Префиксное дерево
- Третичное поисковое дерево
- Union-Find (задача динамической связности)
- Проверка правильности скобок
- Генерация последовательности скобок
- Алгоритм Бойера-Мура
- Динамическое программирование
- QuickSort
- Красно-черные деревья
Merge Sort
Главный недостаток - необходимость использовать дополнительную память для массива размером N, куда мержим. Можно использовать только размер N/2, если копировать в него левый массив и потом мержить этот дополнительный массив и правый массив сразу в оригинал, так что заполняться будет сначала левая половина, потом правая. Это нам сэкономит и память и не надо будет потом смерженный массив копировать в оригинал, так как мы сливаем сразу в оригинале.
Есть два стандартных подхода к реализации - TopDown и BottomUp
TopDown - обычный, через рекурсию
BottomUp - заводим k, на каждой итерации массив делится на блоки размером 2^k (на первой итерации - 2^0=1), мержим соседние блоки.
BottomUp по сути делает тоже самое, что и TopDown, только без использования рекурсии, поэтому рекомендуется использовать его.
In-place реализация
На практике не используется из-за огромных накладных расходов.
Идея в том, что если у нас есть дополнительная память размером N, в которой допустимо перемешать ключи, то мы можем использовать ее в качестве рабочей области.
Итак, мы сливаем наши два массива, а результат не просто пишем в доп. память, а свапаем с тем значением, которое находится. В конце меняем содержимое доп. памяти и наших двух массивов. Теперь важно, что в качестве этой доп. памяти мы можем использовать еще не отсортированную половину нашего сортируемого массива, например, для сортировки правой половины использовать левую, но второй раз этот трюк использовать не получится, так как если мы теперь для сортировки левой будем использовать уже отсортированную правую, то в ней перемешаются ключи.
Теперь сам алгоритм:
- Сортируем правую половину, используя левую в качестве рабочей области
- Левую половину делим еще на две половины и сортируем левую половину левой половины, используя правую половину левой половины в качестве раб. области
- Теперь у нас отсортирована первая 1/4, потом неотсортированная 1/4, потом отсортированная 1/2. Мы мержим обменами сортированную четвертинку и половинку, а выходной итератор устанавливаем в начало несортированной области. После этого у нас сначала идет несортированная 1/4, потом сортированные 3/4.
- Делим несортированную 1/4 на 2 половины и повторяем шаги со 2 по 4, но уже для массива размером в 1/4 от общей длины массива. Продолжаем, пока несортированная часть не станет совсем маленькой, после чего вставляем эту часть в сортированный массив, как в методе вставки.
Достоинства:
- работает на устройствах последовательного доступа
- хорошо сочетается с подкачкой и кэшированием памяти
- можно легко параллелить
- не имеет "трудных" входных данных
- стабильная
Selection sort
Идем слева направо, ищем минимальный элемент в неотсортированной части массива, когда находим - свапаем с самым правым элементом несортированной части. Этот легче всего реализовать на бумажке.
Insertion sort
Идем слева направо, берем самый левый элемент несортированной части и проходим справа налево по сортированной, ищем где его место. Когда находим место - вставляем туда, сдвигая элементы сортированной части направо.
Сильно ускорить можно, если при обмене не менять значения, а просто сдвигать левый направо. Элемент, для которого ищем место, все равно держим в памяти, поэтому в конце просто ставим его в найденное место.
Shellsort
Сложность в лучшем случае: O(n log n)
В худшем: O(n log^2 n) - для лучшей известной последовательности пропусков
В среднем случае - зависит от последовательности пропусков.
Совершенствует Insertion Sort. Проблема Insertion Sort в том, что он всегда сравнивает только соседние элементы, поэтому он очень хорошо работает на почти упорядоченном массиве и очень плохо - на обратно упорядоченном.
Shellsort делает несколько проходов Insertion Sort, но на каждом он сортирует каждый k-й элемент массива, постепенно уменьшая k до 1. Этого можно достигнуть, если в условиях внутреннего цикла Insertion Sort уменьшать индекс при каждой итерации не на 1, а на k.
Есть много вариантов последовательностей k, самая производительная на сегодняшний день такова: [701, 301, 132, 57, 23, 10, 4, 1].
Heap
Представляем дерево в виде массива, у которого a[0] - корень, а для a[i] дочерними являются элементы a[2*i+1], a[2*i+2].
Свойства кучи:
- Значение в любой вершине не меньше, чем значения её потомков.
- Глубина всех листьев (расстояние до корня) отличается не более чем на 1 слой.
- Последний слой заполняется слева направо без «дырок».
Свойства 2 и 3 выполняются автоматически, когда храним кучу в массиве.
Для выполнения свойства 1 нужно при каждом изменении элементов вызывать функцию Heapify. Она работает так:
Если i-й элемент меньше, чем любой из его сыновей, то меняем местами i-й элемент с наибольшим из его сыновей, после чего выполняем Heapify для этого сына.
Если же i-й элемент больше своего родителя, то меняем его местами с родителем и вызываем Heapify для родителя.Добавление
Кладем элемент в конец массива и вызываем Heapify на этом элементе
Инициализация
Чтобы построить кучу из массива, нужно просто вызвать Heapify для всех его элементов, начиная с последнего и кончая первым. Более того, так как начиная с N/2 все элементы - листья, не содержащие потомков, то можем начинать сразу с N/2. В этом случае дерево будет построено за O(N).
Удаление максимума
Ставим последний элемент на место первого, уменьшаем размер, вызываем Heapify(0).
Heap Sort
Использует бинарное сортирующее дерево (она же куча).
Сам алгоритм состоит из 2 этапов:
- Строим кучу (О(n) операций)
- Удаляем по одному элементу за раз и перестраиваем дерево. Только удаленные элементы мы будем класть сразу в конец нашего массива, в котором и хранится дерево. То есть сначала меняем местами
a[0]иa[n-1], перестраиваем дерево, состоящее из элементовa[0] ... a[n-2]. Потом меняем местамиa[0]иa[n-2], перестраиваем деревоa[0] ... a[n-3]и так далее (О(n log n) операций).
Достоинства:
- сортирует на месте, если хранить и дерево и результат в одном массиве
- всегда работает с одинаковой сложностью
Недостатки:
- неустойчив
- на почти отсортированных работает так же, как и на хаотичных
- выборка делается хаотично по всему массиву, поэтому плохо сочетается с кэшированием и подкачкой
- не работает на связанных списках и других структурах последовательного доступа
- из-за сложности выигрыш начинается только от больших n (от нескольких тысяч)
Quick Sort
Разбиение Ломуто
Проще в реализации, но менее эффективно.
algorithm partition(A, lo, hi) is
pivot := A[hi]
i := lo
for j := lo to hi - 1 do
if A[j] ≤ pivot then
swap A[i] with A[j]
i := i + 1
swap A[i] with A[hi]
return iРазбиение Хоара
Данная схема использует два индекса (один в начале массива, другой в конце), которые приближаются друг к другу, пока не найдётся пара элементов, где один больше опорного и расположен перед ним, а второй меньше и расположен после. Эти элементы меняются местами. Обмен происходит до тех пор, пока индексы не пересекутся. Очень важно в качестве изначальной pivot-точки брать именно серединную, а в циклах сдвига left и right делать строгое меньше и строгое больше, это гарантирует нам что они остановятся в середине, а не пойдут в другую половину и не улетят за край массива. Алгоритм возвращает последний индекс. Схема Хоара эффективнее схемы Ломуто, так как происходит в среднем в три раза меньше обменов (swap) элементов, и разбиение эффективнее, даже когда все элементы равны.
algorithm partition(A, lo, hi) is
pivot := A[(hi+lo)/2]
i := lo - 1
j := hi + 1
loop forever
do
i := i + 1
while A[i] < pivot
do
j := j - 1
while A[j] > pivot
if i >= j then
return j
swap A[i] with A[j]Опорный элемент остается в начале, таким образом попадает в подмножество чисел, которые меньше или равны опорному.
Варианты улучшения
- Insertion Sort на малых подмассивах
- Использовать в качестве
pivot-точки медиану из первого, последнего и серединного значения массива - Если в массиве есть множество элементов с одинаковыми ключами, то можно разбивать на 3 партишна, посередине - с элементами, равными
pivot. Это можно сделать разбиением Ломуто, только нужно вести 2 счетчика, один вначале серединного партишна и идет слева направо, другой - в конце серединного партишна и идет справа налево - можно уменьшить рекурсивный стек, чтобы он всегда был O(log n) даже для несбалансированного дерева сравнений. Для этого на каждом этапе первый рекурсивный вызов делать для той части массива, которая длинее, а второй вызов элиминировать как хвостовую рекурсию. Если их не менять местами, то дерево получится опять не сбалансировано, так как например в левой части много элементов, в правой 1, мы элиминировали хвостовую рекурсию для правой части, но ничего от этого не выиграли, т.к. там 1 элемент. (можно конечно совсем избавиться от рекурсии, создав ручной стэк и кладя туда элементы, но так мы потратим столько же памяти, сколько и на рекурсивный стек, хотя рекурсии и не будет)
Radix Heap
(http://ssp.impulsetrain.com/radix-heap.html)
Монотонная очередь с приоритетом. Все ключи должны быть натуральными числами. Разница между максимальным и минимальным ключом не больше определенной константы. Свойство монотонности означает, что нельзя добавлять элементы с ключом, меньшим, чем все имеющиеся к куче ключи.
Сложность операций зависит от разницы между максимальным и минимальным элементом в куые.
Все элементы лежат по бакетам, как в Dictionary. Отдельно хранится переменная last_deleted. Элементы, лежащие в бакете k должны отличаться от last_deleted в бите с номером k-1 (нумерация с 0/с самого младшего бита), могут отличаться в битах, младших чем k-1 и не должны отличаться в битах, старших чем k-1.
Например, пусть в last_deleted лежит 8 и мы пытается посчитать, в каком бакете лежит 10.
8 = 01000
10 = 01010Нам нушно найти самый старший бит, в котором они различаются, поэтому идем от самого старшего к самому младшему.
4: 0 == 0
3: 1 == 1
2: 0 == 0
1: 0 != 1Значит самый старший отличающийся бит имеет индекс 1, а бакет имеет номер 1 + 1 = 2.
Посчитаем, куда идет ключ 30:
8 = 001000
30 = 011110
5: 0 == 0
4: 0 != 1
k - 1 = 4, k = 5Получили пятый бакет.
Теперь рассмотрим операции:
Вставка
Тут все просто - вычисляем номер бакета и добавляем в него. Номер бакета можно вычислить через XOR:
bucket_no = highest_bit (new_element XOR last_deleted) + 1ВАЖНО если на вход функции highest_bit поступает 0, то она должна возвращать -1!
Извлечение
Находим минимальный бакет, в котором есть элементы, затем линейным поиском ищем в этом бакете минимальный элемент и возвращаем, попутно записав его в last_deleted. После этого нам нужно перераспределить оставшиеся элементы в этом бакете в соответствии с новым last_deleted, но остальные бакеты перераспределять не надо, так как младшие и так уже пустые, а для старших ничего не изменилось, их не совпадающие биты все еще не совпадают.
Counting Sort
Алгоритм сортировки для небольших положительных целых чисел.
Для работы понадобится массив с размером, равным максимально возможному используемому числу. Поэтому применение этого алгоритма целесообразно лишь тогда, когда сортируемые числа имеют (или их можно отобразить в) диапазон возможных значений, который достаточно мал по сравнению с сортируемым множеством. Например, миллион натуральных чисел, меньших 1000.
Состоит из 3 шагов:
- Вычисление частот
- Вычисление индексов
- Заполнение результата
function countingSort(array, k) is
count ← new array of k zeros
for i = 1 to length(array) do
count[array[i]] ← count[array[i]] + 1
for i = 2 to k do
count[i] ← count[i] + count[i - 1]
for i = length(array) downto 1 do
output[count[array[i]]] ← array[i]
count[array[i]] ← count[array[i]] - 1
return outputПосле первого цикла в массиве count хранится для каждого числа количество, сколько раз оно встречается во входном массиве.
Во втором цикле мы записываем в массив count т.н. префиксные суммы и после его завершения i-е значение массива означает, сколько чисел в исходном массиве меньше, чем i. То есть это индекс, на котором должно стоять i в результирующем упорядоченном массиве.
В третьем цикле мы заполняем результирующий массив в соответствии с полученным массивом count. Мы берем очередное число из входного массива, смотрим какой записан для него индекс в массиве count и записываем число в результат по этому индексу. После этого индекс в count нужно увеличить, атк как следующее такое число нужно записывать уже на следующую позицию. Сложная логика в этом цикле обусловлена тем, что обычно мы сортируем не просто целые числа, а некие объекты, у которых ключами являются целые числа. Кроме того так мы обеспечиваем стабильность сортировки.
Если же мы сортируем просто целые числа, то мы сразу после первого цикла можем идти по массиву count и вставлять в результат count[i] копий числа i.
Radix Sort
Предназначен для сортировки целых чисел, или же любых объектов, которые можно представить в виде целых чисел. Но сложность алгоритма зависит от длины ключа, поэтому лучше чтобы он был не сильно большой.
Исходя из этого, алгоритм часто используют для сортировки строк.
Алгоритм хорош тем, что его сложность составляет O(n * m), где n - количество элементов, а m - количество знаков в них. В то же время сложность остальных алгоритмов, основанных на сравнении, не может быть ниже чем O(n * log n).
Бывают 2 вида: least significant radix (LSD) и most significant radix (MSD).
LSD
Для алгоритма нужно выбрать значение r, то есть по какому основанию мы будем работать с числами. Вместе с тем это и количество бакетов. При маленьких r алгоритм становится все больше похож на Counting Sort. Ну и вообще, в своей эффективной реализации алгоритм использует Counting Sort, просто повторяет ее для каждого разряда.
Суть алгоритма в том, что мы сначала сортируем по самому младшему разряду, потом по следующему и так до самого старшего.
Например, отсортируем следующий массив (r=10):
170, 45, 75, 90, 2, 802, 2, 66
Сортируем сначала по самому младшему разряду:
170, 90, 02, 802, 2, 45, 75, 66
Теперь по второму:
02, 802, 02, 45, 66, 170, 75, 90
И наконец по третьему:
002, 002, 045, 066, 075, 090, 170, 802
Неэффективная реализация
Самая простая, неэффективная реализация использует массив очередей (или других массивов), где в очереди i лежат элементы, у которых в разряде, соответствующем текущей итерации, записано i.
В нашем примере после первого прохода получим следующий массив очередей:
0: 170, 090
1:
2: 002, 802, 002
3:
4:
5: 045, 075
6: 066
7–9: Затем по порядку вычитываем элементы в одномерный массив:
170 090 002 802 002 045 075 066Затем опять записываем в массив очередей, ориентируясь уже на второй справа разряд:
0: 002, 802, 002
1–3:
4: 045
5:
6: 066
7: 170, 075
8:
9: 090Выписываем в 1-мерный массив:
002 802 002 045 066 170 075 090Третий проход:
0: 002, 002, 045, 066, 075, 090
1: 170
2–7:
8: 802
9: Выписываем результат:
002 002 045 066 075 090 170 802Эффективная реализация
Проходим по знакам в числах от наименее значимого к наиболее значимому и для каждого осуществляем Counting Sort.
Если в качестве r использовать степени двойки, то разряды будет очень удобно получать двоичными операциями сдвига и XOR:
b = количество бит в двоичной записи r
mask = 1 << b
shift = 0
for ...
c = (a[i] >> shift) & mask
shift += bMSD
Все в основном то же самое, но сортировать начинаем с самого значимого знака. Не гарантирует стабильность. Используется, когда нам нужно, например, отсортировать строки по N первых символов. На каждом этапе разбивает массив на несколько подмассивов (по одному на каждый символ алфавита), которые потом можно сортировать рекурсивно. То есть лучше параллелится, чем LSD.
Одновременный поиск минимума и максимума в массиве
Если искать простым линейным поиском, то получим сложность O(2n-1) (количество сравнений в худшем случае). Но есть более эффективный алгоритм со сложностью O(3n/2):
- Разбиваем массив на подмассивы по 2 элемента.
- Упорядочиваем каждый из них (n/2 сравнений). После этого у нас на нечетных местах стоят минимальные элементы из пар, а на четных - максимальные.
- Находим минимальный среди всех нечетных (n/2 сравнений). При этом если количество элементов нечетное, то взять в качестве начального значения последний элемент.
- Находим максимальный среди всех четных (n/2 сравнений). При этом если количество элементов нечетное, то взять в качестве начального значения последний элемент.
Итого - 3n/2 сравнений.
Поиск n-го наименьшего элемента массива без сортировки
Обычно требуется найти такой элемент за время O(n), а сортировка потребует O(n * log n).
Quickselect
Самым популярным алгоритмом тут является Quickselect (от создателя Quicksort). Он работает по тому же принципу что и Quicksort, но на каждом этапе продолжает работать только с одним из полученных партишнов, за счет этого и получается снижение сложности до O(N) в среднем и O(N^2) - в худшем случае.
Медиана медиан
Еще есть алгоритм, который обеспечивает O(N) даже в худшем случае. Он похож на Quickselect, но в качестве pivot-точки на каждом этапе выбирается медиана медиан. Для того чтобы ее найти, мы разбиваем массив на подмассивы по 5 элементов, каждый из них сортируем методом вставки (Insertion sort) и выбираем медиану. Затем формируем массив найденных медиан, и рекурсивно ищем его медиану. Когда массив медиан становится <= 5, то используем Insertion sort чтоб найти его медиану. В результате получаем индекс медианы медиан, который используем как точку pivot.
Засчет того, что точка pivot у нас всегда является медианой массива, худший случай становится средним и мы получаем сложность O(N) в худшем случае. На практике большое количество операций для поиска точки разбиения сильно раздувает константу и этот метод практически не используется.
Выбор 5 в качестве длины группы объясняется тем, что:
- в массивах нечетной длины легче искать медиану, т.к. в четных приходится брать середину двух срединных элементов
Хэш-таблица с открытой адресацией
Обычная хэш-таблица имеет закрытую адресацию - это когда в случае коллизии элемент кладется в список.
В случае открытой адресации при коллизии берется какой-то другой элемент этого же массива. Например, следующий. Если он тоже занят - то следующий за ним. Так как есть коэффициент заполнения, то пустой элемент рано или поздно будет найден.
В случае чтения - точно так же, находим нужный элемент, сравниваем ключ, если не равен - берем следующий, и так пока не найдем нужный.
Когда берем следующий элемент - это называется линейный поиск (Linear probing).
Квадратичный поиск (Quadratic probing) - это когда интервал увеличивается как значение некоторого полинома второй степени.
При использовании метода двойного хэширования (иногда его называют Rehashing) интервал вычисляется с помощью еще одной хэш-функции. Этот метод приводит к уменьшению коллизий, так как следующий проверяемый элемент зависит от самого ключа. Даже если два разных ключа дают один и тот же хэш, то последовательность просматриваемых элементов для них будет разная.
Префиксное дерево
Дерево для хранения данных, ключами которых являются строки. Для каждого узла ребра, соединяющие его с сыновьями, помечены разными символами. Узлы соответствующие концу слова, должны быть помечены. Чтобы найти элемент, нужно начинать с корня и выбирать на i-м уровне то ребро, которое помечено i-м символом в искомом ключе.
Таким образом, ключ, идентифицирующий некий узел, не явно хранится в каком-либо узле, а задается положением узла в дереве. Ключ корня - пустая строка.
Третичное поисковое дерево
Тоже дерево для хранения данных со строковыми ключами. Альтернатива префиксным деревьям, тоже может использоваться для автокомплишена.
Каждый узел хранит символ c и ссылки на 3 дочерних узла. Слева - все ключи, у которых следующий символ меньше текущего, справа - больше, посередине - равны. Таким образом, влево и вправо мы идем, если нас не устраивает текущий символ, а посередине идем, если он устроил, мы его дописываем к текущему ключу.
Пример:
c
/ | \
a u h
| | | \
t t e u
/ / | / |
s p e i sВ этом дереве записаны слова: "cute","cup","at","as","he","us" и "i".
Эта структура имеет большую сложность поиска, чем префиксное дерево, но при этом для не сильно больших словарей занимает гораздо меньше места, так как для каждого узла хранится всего 3 указателя, а не столько, сколько символов есть в алфавите.
Union-Find (задача динамической связности)
Дано N точек с идентификаторами от 0 до N-1. Затем дается список связей между этими точками. Связи транзитивные, то есть если А связано с Б, а Б с В, значит А связано с В. Если на вход подается связь между точками А и Б, а они уже связаны, то эта пара игнорируется. Иначе - точки связываются. В конце выдать, сколько получилось кластеров и каких.
Воспользуемся тем, что точки имеют идентификаторы от 0 до N-1 и будем хранить их в массиве на N элементов. Индекс - идентификатор точки, а значение - идентификатор предыдущего элемента кластера, как если бы элементы кластера были представлены в виде связных списков.
На самом деле для удобного объединения кластеров мы будем хранить их в деревьях, но деревья будут представлены в виде массивов. Каждый элемент хранит индекс родительского элемента, а если индекс элемента равен самому элементу, значит этот элемент - корень своего кластера.
Для поиска, какому кластеру принадлежит элемент, нам нужно "подниматься" в дереве от этого элемента, пока не достигнем корня. А чтобы объединить кластеры, нужно всего лишь корню одного кластера присвоить значение корня другого.
Тогда операции объединения и поиска будут выглядеть так:
public int find (int id) {
var p = id;
while (_ids[p] != p) p = _ids[p];
return p;
}
public void union (int a, int b) {
int ca = find (a),
cb = find (b);
if (ca == cb) return;
_ids[ca] = cb;
}В операции union есть недостаток - мы не знаем, какой из кластеров больше и в результате у нас получается несбалансированное дерево, по которому операция find будет выполняться все дольше и дольше. Для решения проблемы мы можем завести отдельный массив, где храним веса кластеров и всегда мержить меньший кластер к бОльшему.
Проверка правильности скобок
Написать функцию, проверяющую правильно расставленные скобки;
check("{()}[]") // true check("{[}]") // falseТут решается простым стэком, в котором мы храним открывающие скобки. Когда встречаем открывающую - пушим в стек. Когда встречаем закрывающую - проверяем, что матчится с той, которая лежит на вершине стека и если да, то попим из стэка.
Самое главное:
- если у нас закрывающая скобка, то сначала проверить, что в стэке еще есть элементы!
- когда строка закончилась, проверить что стэк пуст, иначе возвращаем false!
Генерация последовательности скобок
Делаем через рекурсию, других способов не знаю. Только надо помнить, сколько скобок уже открыли и сколько закрыли. И еще важно НЕ ставить else между рекурсивными вызовами Generate.
if (i == 2 * n) {
result.Add (new string (a));
return;
}
if (open < n) {
a[i] = '(';
Generate (result, a, i + 1, n, open + 1, close);
}
if (close < open) {
a[i] = ')';
Generate (result, a, i + 1, n, open, close + 1);
}Дерево отрезков
Структура данных, позволяющая за время O(log n) получить значение некой функции для любого последовательного интервала элементов массива.
Например, у нас есть массив:
4, 7, -12, 23, -9, 19, 0, 22, 7, 6, -4, 15Дерево отрезков поможет нам быстро найти значение некой аггрегирующей функции (например, поиск минимума/максимума, сумма, произведение) для любого подмассива, например, для [7, -12, 23, -9, 19] или [-9, 19, 0] или любого другого.
Поддерживается операция обновления (тоже O(log n)).
Рассмотрим работу алгоритма на примере подсчета суммы элементов.
В корне дерева хранится сумма всех элементов массива. В левом ребенке - сумма элементов левой половины, в правом - элементов правой. И так далее рекурсивно вниз, а в листьях хранятся значения функции над единичным интервалом, то есть в случае суммы- сами единичные элементы.
Строится дерево снизу вверх - сначала заполняем нижний уровень, затем считаем значения предыдущего уровня как сумму двух листьев, затем предыдущего и так далее. Строится такое дерево за O(n).
При запросе суммы мы принимаем на вход интервал [l..r], для которого посчитать сумму, встаем в корень дерева и сначала смотрим, совпадают ли границы интервала, соответствующего корню, границам искомого отрезка. Если да - то просто возвращаем значение корня. Если же нет, то смотрим, в какие из двух сыновей попадает отрезок [l..r]. Если он целиком попадает в одного из сыновей, то рекурсивно запускаем запрос для этого сына. Если же он пересекается с обоими, то рекурсивно запускаем запрос по левому дереву для отрезка [l..n/2], потом по правому по отрезка [n/2+1..r] и суммируем результаты.
Хранится дерево отрезков обычно в виде массива (по аналогии с кучей), где в каждом элементе хранится значение функции над соответствующим элементу интервалом, а детьми элемента с индексом i являются элементы 2*i+1 и 2*i+2. Для массива длиной n количество будет не больше, чем 2n, НО для массива нужно выделить длину 4n, потому что дерево получится несбалансированное и индексы нижнего уровня могут выходить за пределы 2n.
Построение
a - исходный массив, v - текущая вершина, tl и tr - границы отрезка, соответствующего текущей вершине дерева. Из основной программы вызывается с параметрами: v=0, tl=0,tr=n-1.
void build (int a[], int v, int tl, int tr) {
if (tl == tr)
t[v] = a[tl];
else {
int tm = (tl + tr) / 2;
build (a, v*2, tl, tm);
build (a, v*2+1, tm+1, tr);
t[v] = t[v*2] + t[v*2+1];
}
}Запрос суммы
v - текущая вершина, tl и tr - границы отрезка, соответствующего текущей вершине дерева, l и r - границы запроса. При первом запуске подаются параметры v=0, tl=0, tr=n-1.
int sum (int v, int tl, int tr, int l, int r) {
if (l > r)
return 0;
if (l == tl && r == tr)
return t[v];
int tm = (tl + tr) / 2;
return sum (v*2, tl, tm, l, min(r,tm))
+ sum (v*2+1, tm+1, tr, max(l,tm+1), r);
}Запрос модификации
v - текущая вершина, tl и tr - границы отрезка текущей вершины, pos - индекс меняющегося элемента, new_val - его новое значение.
void update (int v, int tl, int tr, int pos, int new_val) {
if (tl == tr)
t[v] = new_val;
else {
int tm = (tl + tr) / 2;
if (pos <= tm)
update (v*2, tl, tm, pos, new_val);
else
update (v*2+1, tm+1, tr, pos, new_val);
t[v] = t[v*2] + t[v*2+1];
}
}Алгоритм Кнута-Морриса-Пратта
Алгоритм поиска подстроки длиной n в строке длиной m. Основывается на префикс-функции. Решает задачу за O(n+m) и O(n) памяти.
Префикс-функция
Для строки s длиной n префикс-функция это такой массив p длиной n, в котором p[i] означает длину наибольшего нетривиального (не равного самой строке) префикса, совпадающего с суффиксом для строки s[0..i]
Например, для строки "abcabcd" префикс-функция равна: [0, 0, 0, 1, 2, 3, 0], что означает:
- у строки "a" нет нетривиального префикса, совпадающего с суффиксом;
- у строки "ab" нет нетривиального префикса, совпадающего с суффиксом;
- у строки "abc" нет нетривиального префикса, совпадающего с суффиксом;
- у строки "abca" префикс длины 1 совпадает с суффиксом;
- у строки "abcab" префикс длины 2 совпадает с суффиксом;
- у строки "abcabc" префикс длины 3 совпадает с суффиксом;
- у строки "abcabcd" нет нетривиального префикса, совпадающего с суффиксом.
Нахождение префикс-функции
Этот алгоритм не содержит явных сравнений строк и выполняет O(n) действий.
Пусть мы, идя от s[0] к s[n] дошли до некоторого индекса i и вычислили его префикс-функцию p[i] = j.
Тогда для i+1 префикс-функция увеличится на 1 только в том случае, если s[i+1] == s[j]. (1)
Если же они не равны, то нам нужно найти такое значение k, которое меньше p[i], но при этом для него все еще выполняется условие "префикс равен суффиксу", и когда мы найдем такое значение, сможем попробовать условие s[i+1] == s[k] для него. То есть мы знаем, что s[0..j-1] == s[i-j..i-1] и нам нужно найти k, такое, что k<j и s[0..k-1] == s[i-k..i-1]. Но у нас уже есть такое значение, мы его получили, когда вычисляли префикс-функцию для строки s[0..j-1]. Поэтому берем j=p[j-1] и проверяем, выпонляется ли условие 1: s[i+1] == s[j]. Если нет, то повторяем уменьшение j, пока не дойдем до нуля.
Итак, получили такой алгоритм:
- Считать значения префикс-функции
p[i]будем по очереди: отi=1кi=n-1(значениеp[0]просто присвоим равным нулю). - Для подсчёта текущего значения
p[i]мы заводим переменнуюj, обозначающую длину текущего рассматриваемого образца. Изначальноj = p[i-1]. - Тестируем образец длины
j, для чего сравниваем символыs[j]иs[i]. Если они совпадают — то полагаемp[i] = j+1и переходим к следующему индексуi+1. Если же символы отличаются, то уменьшаем длинуj, полагая её равнойp[j-1], и повторяем этот шаг алгоритма с начала. - Если мы дошли до длины
j=0и так и не нашли совпадения, то останавливаем процесс перебора образцов и полагаемp[i] = 0и переходим к следующему индексуi+1.
Алгоритм требует хранения самой строки и предыдущих вычисленных значений префикс-функции, однако, как нетрудно заметить, если нам заранее известно максимальное значение, которое может принимать префикс-функция на всей строке, то достаточно будет хранить лишь на единицу большее количество первых символов строки и значений префикс-функции.
Поиск подстроки
Допустим, нам надо найти подстроку s длиной n в тексте t. Для этого мы:
- выбираем некий специальный символ
#, которого точно нет ни вs, ни вt - составляем строку
Q = s + "#" + t - вычисляем префикс-функцию
PдляQ - просматриваем значения
P, начиная с индексаn+1. Там, гдеP[i] == n-iобозначает индекс очередного вхожденияsвt, а начало вхождения будет по индексуi - (n + 1) - n + 1 = i - 2n.
Количество различных подстрок в строке
Допустим, мы знаем текущее количество подстрок и хотим посчитать новое количество при добавлении одного символа (допустим, это символ c).
В идеале при добавлении символа c к строке s длиной n мы получаем n+1 новых подстрок, каждая из которых оканчивается на c. (не обязательно различных).
Теперь узнаем, какие из них уже были в строке s.
Для этого мы добавляем символ c, разворачиваем полученную строку s+c и ищем для нее префикс-функцию. Она нам покажет, встречались ли уже внутри s каждая из подстрок, оканчивающихся на c . Найдя максимум префикс функции m=max(p[0..n]), мы можем быть уверены, что подстрока длиной m, оканчивающаяся на символ c уже встречалась ранее в строке s, а значит и все строки длиной 1..m тоже там встречались.
Итак, при добавлении 1 символа добавляются s.length + 1 - max(p[0..s.length + 1]) различных подстрок.
Построение префикс функции - O(n), выполнение вышеописанной операции для каждого символа - O(n), итого получили O(N^2).
Алгоритм Бойера-Мура
Алгоритм поиска подстроки в строке, считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке.
Суть алгоритма в том, что мы идем по тексту слева направо (допустим, переменной i), а с паттерном сверяем справа налево (допустим, переменной j). Как только встречаем несовпадающий символ (допустим, в паттерне p, а в тексте c) - шаблон сразу сдвигается на несколько символов вправо и сверять начинаем опять с конца.
Важно то, как определить, сколько символов эти несколько:
- если в паттерне вообще нет символа
c- сдвигаем паттерн наj+1 - если есть, то сдвигаем на
jминуc самая правая позиция, в которойcвстречается в паттерне. Чтобы знать эти значения, таблица таких позиций составляется заранее - если же паттерн в результате не сдвинулся вправо (сдвиг получился меньшим или равным нулю), принудительно его сдвигаем на 1 позицию
BoyerMoore(String pat)
{ // Compute skip table.
this.pat = pat;
int M = pat.length();
int R = 256;
right = new int[R];
for (int c = 0; c < R; c++)
right[c] = -1; // -1 for chars not in pattern
for (int j = 0; j < M; j++) // rightmost position for
right[pat.charAt(j)] = j; // chars in pattern
}
public int search(String txt)
{ // Search for pattern in txt.
int N = txt.length();
int M = pat.length();
int skip;
for (int i = 0; i <= N-M; i += skip)
{ // Does the pattern match the text at position i ?
skip = 0;
for (int j = M-1; j >= 0; j--)
if (pat.charAt(j) != txt.charAt(i+j))
{
skip = j - right[txt.charAt(i+j)];
if (skip < 1) skip = 1;
break;
}
if (skip == 0) return i;
}
return N;
}Двоичное дерево
В левом поддереве - значения строго меньше корня. В правом - больше или равные корню.
Здесь самое сложное - это удаление.
Удаление элемента
Сначала находим удаляемый узел.
Если детей у него нет - прекрасно, просто удаляем.
Если есть один ребенок - тоже неплохо, удаляем узел, ставим вместо него ребенка.
Если же 2 ребенка, то берем следующий по возрастанию элемент, а это будет самый левый узел правого поддерева удаляемого узла, и ставим его на место удаляемого, не забыв связать с детьми.
А если у правого поддерева нет левого узла, то ставим правого ребенка удаляемого узла на место удаляемого.
Динамическое программирование
Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А.Кумок
Способ решения сложных задач путем разбиения их на более простые подзадачи. Применим к задачам с оптимальной подструктурой, выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной.
Задача имеет оптимальную подструктуру, если её оптимальное решение может быть рационально составлено из оптимальных решений её подзадач.
Два главных приема, используемых в динамическом программировании:
- Мемоизация
- Восходящий анализ
Например, такая задача: есть доска, игрок стартует в левом верхнем углу, может идти только вниз и направо. Посчитать количество маршрутов до правого нижнего угла.
Легко заметить, что количество маршрутов в любую точку можно получить как сумму количества маршрутов в соседнюю сверху и соседнюю слева точку. Но если мы будем решать задачу рекурсивно "сверху вниз", то это будет слишком неэффективно, поэтому задачи динамического программирования обычно решаются "снизу вверх" (в этом случае обязательно должны быть заданы начальные состояния), как здесь:
int[][] dp = new int[Imax][Jmax];
for(int i=0; i<Imax; i++){
for(int j=0; j<Jmax; j++){
if(i==0 || j==0){
dp[i][j]=1; // Если это левая или верхняя граница, то есть только один способ туда попасть. Это и есть наши начальные состояния.
}else{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
}
System.out.println(dp[Imax-1][Jmax-1]);Другая задача:
При переработке радиоактивных материалов образуются отходы двух видов — особо опасные (тип A) и неопасные (тип B). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A. Стопка считается безопасной, если она не является взрывоопасной. Для заданного количества контейнеров N определить количество возможных типов безопасных стопок.
Здесь количество способов сложить стопку высотой i складывается из
- количества стопок высотой i-1, на которые мы можем положить B
- количества стопок высотой i-1 с контейнером В на вершине, на который мы можем положить А
Второе количество в свою очередь получается как количество стопок высотой i-2, так как на каждую такую стопку мы можем положить сверху контейнер В
Итак, получили такой алгоритм:
static int Calculate (int n) {
int[] a = new int[n + 1];
a[0] = 1;
a[1] = 2;
for (int i = 2; i <= n; i++) {
a[i] = a[i - 2] + a[i - 1];
}
return a[n];
}Решатель математических выражений
Разберем парсинг и решение выражений на примере самой базовой формы - когда все операторы разделены пробелами, а пары операторов - скобками. Нам нужно понять только основной принцип, поэтому остальное бдует мешать.
Пример входа:
( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )Алгоритм
Заводим 2 стэка - один для операндов, другой для операторов.
Проходим по всем токенам слева направо.
Если текущий токен - число: пушим его в стэк операндов
Если текущий токен - оператор: пушим его в стэк операторов
Если текущий токен - закрывающая скобка: попаем 2 операнда и один оператор, выполняем соответствующую операцию, результат пушим в стэк операндов
Если текущий токен - открывающая скобка: игнорируем
Когда закончим итерировать по выражению, если оно составлено правильно, то в стэке операторов останется один элемент, который и будет общим результатом.
Графы
Поиск в глубину
- Начинаем с указанной вершины v
- Помечаем v как посещенный
- Выбираем не помеченных соседей v
- Для каждого из них рекурсивно вызываем процедуру поиска (если не нравится рекурсия - можно в стэк складывать вершины, потом возвращаться в пункт 1 и доставать из стэка следующую, только не забыть проверить ее метку, прежде чем начинать с ней работать)
Все!
Применение
- поиск маршрута между вершинами. Для этого в процессе поиска в глубину заводим массив
edgeTo, куда для каждой вершиныwпишем вершинуv, из которой мы в нее пришли. В результате получаем массив, по которому за O(n) можем выдать маршрут (не обязательно кратчайший) из любой вершины в указанную. - поиск связанных компонент. Для этого делаем DFS, после завершения все помеченные вершины будут принадлежать одному связанному компоненту. Чтобы найти остальные - берем первую непомеченную вершину и запускаем поиск в глубину от нее. Лучше всего - идти в цикле по всем вершинам и запускать DFS для непомеченных, так рано или поздно будут помечены все.
- топологическая сортировка. Похоже на поиск связанных компонент, только каждую обработанную вершину кладем в стек, ну или очередь, в зависимости от направления связи. И еще - такой алгоритм сработает только при использовании рекурсии.
- поиск циклов в графе. Похож на поиск маршрута, но основывается на идее что если в текущем стэке нам два раза встретилась одна и та же вершина, значит цикл есть. Поэтому заводим новый массив
bool[] onStack, устанавливаем вtrueтекущую вершину в начале работы с ней, а в конце - ставимfalse, и когда берем очередную вершинуi- проверяем, не равен ли истинеonStack[i]. Если нужно вернуть сам цикл, то поддерживаем еще иedgeToтак же, как и в задаче поиска пути - в направленном графе применяется для поиска достижимых объектов при сборке мусора
Поиск в ширину
Позволяет найти самый короткий маршрут между вершинами. Используется, например, для нахождения числа Кевина Бэйкона.
В целом тоже самое, что и поиск в глубину, только на 4 шаге вместо стэка используем очередь.
Минимальное остовное дерево
Остовное дерево - это дерево, соединяющее все вершины графа. Минимальное остовное дерево взвешенного графа - остовное дерево, имеющее минимальный вес.
Сразу оговоримся, что указанные здесь алгоритмы не работают для направленных графов. Для них проблема носит другое название - minimum cost arborescence problem.
Алгоритм Прима
При количестве ребер, равном Е, алгоритм использует О(E) места и О(E log E) времени.
Сначала берётся произвольная вершина и находится ребро, инцидентное данной вершине и обладающее наименьшей стоимостью. Найденное ребро и соединяемые им две вершины образуют дерево. Затем, рассматриваются рёбра графа, один конец которых — уже принадлежащая вершине дерева, а другой — нет; из этих рёбер выбирается ребро наименьшей стоимости. Выбираемое на каждом шаге ребро присоединяется к дереву. Рост дерева происходит до тех пор, пока не будут исчерпаны все вершины исходного графа.
Здесь главная сложность - в том, чтобы на каждом шаге находить ребро наименьшей стоимости.
Для этого нам понадобятся:
- массив
marked, в котором истиной обозначены те вершины, которые уже внесены в остовное дерево - массив
edgeTo, в который мы будем заносить ребра, внесенные в остовное дерево - очередь с приоритетом
MinPQ<Edge>содержащая все ребра от внесенных вершин к еще не внесенным. Эта очередь позволит нам на каждой итерации брать ребро с наименьшим весом.
При добавлении новой вершины мы добавляем в очередь все ее ребра, которые соединяют ее с вершинами, еще не внесенными в marked.
А еще, когда добавляем новую вершину, то нужно пройтись по очереди приоритетов и удалить ребра, которые содиняют добавленную вершину с добавленными ранее вершинами. Но можно это сейчас не делать, а просто когда достаем ребра из очереди, проверять, что оно соединяет включенную вершину с еще не включенной.
Алгоритм Крускала
Алгоритм Крускала изначально помещает каждую вершину в своё дерево, а затем постепенно объединяет эти деревья, объединяя на каждой итерации два некоторых дерева некоторым ребром. Перед началом выполнения алгоритма, все рёбра сортируются по весу (в порядке неубывания). Затем начинается процесс объединения: перебираются все рёбра от первого до последнего (в порядке сортировки), и если у текущего ребра его концы принадлежат разным поддеревьям, то эти поддеревья объединяются, а ребро добавляется к ответу. По окончании перебора всех рёбер (E=V-1) все вершины окажутся принадлежащими одному поддереву, и ответ найден.
Для поддержания леса деревьев и быстрого поиска циклов можем использовать структуру Union-Find. Либо же простой массив tree_id[n], но линейный поиск по нему навредит нашему перформансу.
Поиск кратчайшего пути в направленном взвешенном графе
Алгоритм Дейкстры
Алгоритм использует O(V) места и O(E log V) времени. Работает, даже если в графе есть циклы.
Находит минимальные расстояния от некой вершины a до всех остальных вершин графа.
Каждой вершине графа сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать (relax) метки. Работа алгоритма завершается, когда все вершины посещены. Теперь подробнее.
Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку (на первом шаге это будет a, так как ее метка равна 0, а метки всех остальных вершин - бесконечности). Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовём соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещённую и повторим шаг алгоритма.
Вообще алгоритм похож на алгоритм Прима, только там на каждом шаге к дереву добавляется вершина, которая ближе всего к дереву, а здесь - та, которая ближе всего к источнику.
Реализация
Нвм понадобятся:
- очередь с приоритетом, чтобы всегда знать, у какой вершины минимальная метка. Причем эта очередь должна поддерживать возможность изменения элементов, а значит поддерживать внутри себя еще словарь, ассоциирующий ключ с индексом элемента во внутренней коллекции.
- массив
distTo[n], в котором для каждой вершины будет храниться ее метка (она же текущее минимальное расстояние от нее доa). Он нам нужен, чтобы, проходя по всем соседям выбранной вершины, знать их метки - массив
edgeTo[n], в котором для каждой вершины хранится ее родительская на кратчайшем пути отaк ней. Этот массив нам нужен, чтобы иметь возможность в конце выдать найденный путь
Быстрый алгоритм для ацикличных графов
Если графов точно нет, то можно воспользоваться гораздо более простым и быстрым алгоритмом:
- массив
distToинициализируется так же, каки в алгоритме Дейкстры - 0 для стартовой вершины, бесконечность для остальных - идем по вершинам графа в порядке топологической сортировки
- для каждой вершины вызываем процедуру ослабления, то есть проходим по всем ребрам, исходящим из нее и для всех вторых вершин смотрим, является ли их текущая метка больше, чем вес ребра плюс метка первой вершины, и если да, то обновляем
LSM-дерево
Состоит из:
- лога на диске, куда последовательно записываются все новые данные
- один большой и несколько маленьких SSTable на диске - индексы по логу
- MemTable - сбалансированное бинарное дерево поиска, хранимое в памяти.
SSTable - представляет из себя последовательные записи ключ-значение, отсортированные по ключу. SSTable иммутабелен, как только он создан и сохранен на диск, он больше никогда не меняется.
SSTable состоит из множества блоков по 64 КБ (настраивается), и индекса в конце. Индекс держится в памяти. Когда нам нужно что-то найти, то проходимся по этому индексу бинарным поиском, узнаем в каком блоке лежит этот ключ, читаем с диска весь блок за раз и последовательно проходим по нему в поисках нужного нам ключа.
Запись
- Пишем данные в лог на диск
- Пишем смещение в логе для этого ключа в MemTable в памяти
- Когда MemTable становится большим - пишем его на диск в виде SSTable. Это легко сделать, так как из дерева поиска легко получить отсортированный массив.
- Когда SSTable-ов становится слишком много, мержим их в один большой сегмент.
Поиск
- Сначала ищем в MemTable
- Если не нашли - ищем в последнем записанном на диск SSTable
- Если не нашли - то в предыдущем, и так далее.
Очень затратно будет искать ключ, которого нет, поэтому обычно для каждого SSTable поддерживается еще фильтр Блума, который позволяет однозначно сказать, если какого-то ключа в индексе нет.
Обновление
Просто пишем новое значение, старое остается на диске, но так как при поиске мы ищем от новых к старым, то старое в дальнейшем будет игнорироваться.
Удаление
Через tombstone.
Сумма двух
Имея массив целых чисел, нужно вернуть индексы двух элементов, сумма которых будет равна заданному числу
Пример
Допустим, у нас есть массив nums == [2, 7, 11, 15] и нужно получить число 9.
Так как nums[0] + nums[1] == 2 + 7 == 9, то возвращаем массив индексов [0,1].
Решение
- Сортируем массив по возрастанию;
- Идем по массиву с двух концов навстречу друг другу счетчиками i (слева) и j (справа);
- Если
nums[i] + nums[j] < target, то увеличиваем i; - Иначе, если
nums[i] + nums[j] > target, то уменьшаем j; - Если же
nums[i] + nums[j] == target, то очевидно возвращаем[i, j].
Самая длинная подстрока без повторяющихся символов
Имея строку, найти в ней самую длинную подстроку без повторяющихся символов.
Примеры
"abcabcbb" => "abc"
"bbbbb" => "b"
pwwkew => "wke"
Решение
Для решения используем так называемое скользящее окно - это подстрока нашей входной строки input, которая не содержит повторяющихся символов, начинается в начале input и постепенно движется (скользит) по направлению к ее концу.
Нам понадобится словарь символов, у которого ключом будет символ, а значением - индекс последнего такого символа в строке, который нам встретился. Назовем этот словарь s. Если известно, что все символы входят в некое подмножество/алфавит (например, символы латинского алфавита a-z), то можно вместо словаря использовать массив на n элементов, где n = длина алфавита.
- Инициализируем
start=0, это будет левая граница нашего скользящего окна. - Идем счетчиком
iс левого края. -
Если
sсодержитinput[i]иs[input[i]]>=start, то мы встретили первый повторяющийся символ в текущем окне.- Длина соответствующей подстроки равна
i-start+1, нужно ее сравнить с текущим максимумом. Если эта длина больше текущего максимума, то запоминаем строку и обновляем максимум. - Теперь нам нужно сдвинуть левый край окна и мы можем его сдвинуть сразу к символу справа от первого (левого) повторяющегося символа из нашей пары, т.к. для любого края левее этого, подстрока уже заведомо будет содержать повторяющийся символ. Таким образом,
start = s[input[i]] + 1.
- Длина соответствующей подстроки равна
- Запоминаем в наше множество индекс текущего символа:
s[input[i]] = i.
Медиана 2 отсортированных массивов
Имея 2 отсортированных массива, найти их медиану. Сложность должна быть O(log(n+m)). Медиана - это число, разделяющее множество на 2 подмножества одинаковой длины, одно из которых всегда меньше другого.
Пример
Для массивов [1, 3] и [2] медиана равна 2.0.
Для [1, 2] и [3, 4] медиана равна (2 + 3) / 2 = 2.5
Решение
Пусть на входе у нас есть массивы a и b, обозначим их длины как m и n соответственно.
Чтобы выполнить условия задачи, нам нужно разбить входное множество, состоящее из элементов массивов m и n на 2 подмножества, удовлетворяющие следующим критериям:
- Критерий равенства длин - в подмножествах одинаковое количество элементов.
- Критерий соотношения граничных элементов отсортированных подмножеств - максимальный элемент левого подмножества должен быть меньше или равен минимальному элементу правого.
Сейчас обьясню, что это значит. Допустим, мы разбиваем массив A в точке i, а массив B в точке j.
left | right
A[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]Тогда условия будут выглядеть так:
len(left) == len(right) -> i + j == (m - i) + (n - j) -> j == (m + n) / 2 - i -> (учтем нечетные длины, прибавив к числителю 1) j == (m + n + 1) / 2 - imax(left) <= min(right) -> A[i-1] <= B[j] && B[j-1] <= A[i]
Если эти условия соблюдены, то искомая медиана будет равна:
median = (max(left) + min(right)) / 2
Значит, задача свелась к следующей:
Найти
iв[0, m], такую, что:A[i-1] <= B[j] && B[j-1] <= A[i] где j = (m + n + 1) / 2 - i
Это мы можем сделать половинным делением.
Когда нашли i, медиана будет равна:
max(A[i-1], B[j-1]), еслиm+nнечетное и(max(A[i-1], B[j-1]) + min(A[i], B[j])) / 2, еслиm+nчетное
Найти подмассив с максимальной суммой
Вариант 1. Разделяй и властвуй
Делим массив на 2 половины и возвращаем максимум из:
- максимальная сумма в левой половине
- максимальная сумма в правой половине
- максимальная сумма в подмассиве, пересекающем середину
1 и 2 пункт - это просто рекурсивные вызовы.
3 пункт посложнее - там нужно от середины идти влево и вправо, и считать масимальную сумму элементов левой и правой половины, а потом суммировать их.
Рассмотрим пример, допустим у нас такой массив:
6 1 -3 4 -1 3 -5 4Максимальная сумма идущих подряд элементов в левой половине = 7 для последовательности 6 1.
Максимальная сумма идущих подряд элементов в правой половине = 4 для последовательности 4.
Максимальная сумма в подмассиве, пересекающем середину - складывается из:
- максимальной суммы идущих подряд элементов левой половины, включающих самый правый элемент левой половины. В данном случае это 8 для последовательности
6 1 -3 4. - максимальной суммы идущих подряд элементов правой половины, включающих самый левый элемент правой половины. В данном случае это 2 для последовательности
-1 3.
Получили максимальную сумму в подмассиве, пересекающем середину = 8 + 2 = 10.
Результат выбираем как максимум из трех полученных максимумов, то есть max(7, 4, 10) == 10, то есть последовательность 6 1 -3 4 -1 3.
Сложность - O(nlogn)
Вариант 2. Алгоритм Кадане.
Алгоритм Кадане - это специализированный алгоритм именно для этой задачи. Объяснять это словами будет тяжело, лучше сразу кодом.
На псевдокоде описывается очень просто:
Initialize:
max_so_far = 0
max_ending_here = 0
Loop for each element of the array:
max_ending_here = max_ending_here + a[i]
if(max_ending_here < 0)
max_ending_here = 0
if(max_so_far < max_ending_here)
max_so_far = max_ending_here
return max_so_farИдея так же проста - идем по массиву скользящим окном, ищем последовательные подмассивы, сумма которых больше нуля и берем максимальную сумму из них.
Пример:
2 -3 8 -1Алгоритм выдаст 8 и это правильно.
Если бы кусок перед 8 выдавал результат больше нуля, то он бы увеличивал масимальную сумму и мы бы его взяли.
Если он меньше нуля, то он точно уменьшает сумму и мы его не берем.
Более сложный пример:
3 2 -7 2 1 -2 4 -1 3 -5 4Идем слева направо, считаем сумму:
3 => max = 3
3 + 2 = 5 => max = 5
3 + 2 - 7 = -2 < 0 начинаем считать заново
2 < max
2 + 1 = 3 < max
2 + 1 - 2 = 1 < max
2 + 1 - 2 + 4 = 5 == max
2 + 1 - 2 + 4 - 1 = 4 < max
2 + 1 - 2 + 4 - 1 + 3 = 7 > max обновляем max = 7
2 + 1 - 2 + 4 - 1 + 3 - 5 = 2 < max
2 + 1 - 2 + 4 - 1 + 3 - 5 + 4 = 6 < maxИтог: максимум = 7 для последовательности 2 1 -2 4 -1 3.
Найти отсутствующий элемент
Есть массив из N-1 различных чисел от 1 до N. Нужно найти отсутствующий элемент.
Решение 1
Суммируем все элементы массива и вычитаем результат из ожидаемой суммы всех чисел от 1 до N, которая равна n \* (n+1) / 2. Результат вычитания будет ответом.
Решение 2
XOR-им все числа от 1 до N, затем поверх этого XOR-им все элементы нашего массива. Результат будет ответом.
Вот почему это работает:
(A1 ^ A2 ^ A3) ^ (A1 ^ A3) = (A1 ^ A1) ^ A2 ^ (A3 ^ A3) = 0 ^ A2 ^ 0 = A2Найти точку эквилибриума в массиве
Точка эквилибриума - это такой элемент массива, у которого сумма всех элементов слева равна сумме всех элементов справа.
Решение 1
Допустим, наш исходный массив input равен [1, 2, 3, 4, 5, 6, 7, 2, 9, 10].
Создаем массив аггрегированных сумм, где каждый i-й элемент равен сумме элементов 0..i-1 исходного массива. Полученный массив sums будет таким: [1, 3, 6, 10, 15, 21, 28, 30, 39, 49]
Теперь идем по input справа налево и так же считаем аггрегированные суммы, но на каждом шаге сравниваем полученный элемент с элементом массива sums, стоящим на 2 позиции левее.
Потом идем по input справа налево, так же считаем подвижную сумму и сравниваем ее с элементом в sums на 2 левее текущего. Как только эти значения становятся равны, мы останавливаемся и выдаем в качестве результата элемент, стоящий между ними.
Для нашего примера, идем по input справа налево и считаем аггрегированную сумму rsum:
- Крайний правый элемент
inputравен 10, значитrsum = 10. Индекс крайнего правого элемента равен 9, сравниваем его сsum[7]==30. 10 < 30, поэтому продолжаем. - Следующий справа элемент
input[8]равен 9, суммаrsumстановится 10+9=19, индекс равен 8, сравниваем сsum[6]==28. 19<28, продолжаем. - Следующий справа элемент
input[7]равен 2, суммаrsumстановится 19+2=21, индекс равен 7, сравниваем сsum[5]==21. 21==21, условие выхода выполнилось. Индекс эквилибриума равен 7-1==6, поэтому возвращаемinput[6] == 7.
Недостаток этого решения в том, что нужен дополнительный массив.
Решение 2
Этот вариант решения сложнее для реализации, но ему не нужен дополнительный массив.
Считаем сумму всех элементов массива sum
leftsum = 0
rightsum = sum
Идем по массиву слева направо, на каждом шаге:
rightsum -= a[i]
Если leftsum == rightsum, то точка эквилибриума найдена
leftsum += a[i]Рассмотрим на нашем примере [1, 2, 3, 4, 5, 6, 7, 2, 9, 10].
| i | a[i] | rightsum | leftsum |
|---|---|---|---|
| - | - | 49 | 0 |
| 0 | 1 | 48 | 1 |
| 1 | 2 | 46 | 3 |
| 2 | 3 | 43 | 6 |
| 3 | 4 | 39 | 10 |
| 4 | 5 | 34 | 15 |
| 5 | 6 | 28 | 21 |
| 6 | 7 | 21 | 21 |
В последней строке суммы сошлись, точка эквилибриума найдена, возвращаем a[i]==7.
External sorting (внешняя сортировка)
Применяется для сортировки огромных массивов данных, которые не уменьшаются в память. Массив делится на чанки, помещающиеся в память, каждый из чанков сортируется и пишется на диск. Затем из каждого файла берется начальный мини-чанк и между мини-чанками производится merging на диск. Когда какой-то из мини-чанков пустеет, он заполняется следующими данными из своего файла.
Пример
Есть 900 МБ файл и 100 МБ памяти.
- Делим файл на 9 чанков по 100 МБ, сортируем каждый quicksort-ом и пишем в отдельный файл на диске.
- Из каждого файла берем первые 10 МБ (мини-чанки) и еще 10 МБ выделяем на выходной буфер.
- Проходим по 9 мини-чанкам, берем первый элемент, ищем минимальный. Когда нашли - аппендим его в выходной буфер, а из мини-чанка удаляем.
- Если после очередного удаления мини-чанк опустел, то заполняем его следующими 10 МБ из его файла.
- Если после очередной записи в выходной буфер он заполнился, то флашим его на диск и очищаем.
Этап мержа (шаг 3) здесь неэффективен, так как требует приблизительно N * (k - 1) сравнений.
Можно на этом этапе использовать min-heap с ключом равным первому элементу чанка.
QuickSort
public static class QuickSort
{
public static void Sort<T>(T[] input) where T:IComparable
{
SortImpl(input, 0, input.Length);
}
private static void SortImpl<T>(T[] a, int lo, int hi) where T : IComparable
{
if (hi - lo <= 1) return;
T pivot = a[lo];
int l = lo, r = hi - 1;
while (l <= r)
{
while (a[l].CompareTo(pivot) < 0 && l < hi) l++;
while (a[r].CompareTo(pivot) > 0 && r >= lo) r--;
if (l <= r)
{
Swap(a, l, r);
l++;
r--;
}
}
Swap(a, lo, l - 1);
SortImpl<T>(a, lo, l);
SortImpl<T>(a, l, hi);
}
private static void Swap<T>(T[] input, int a, int b)
{
T tmp = input[a];
input[a] = input[b];
input[b] = tmp;
}
}Красно-черные деревья
Это бинарные поисковые деревья, удовлетворяющие следующим условиям:
- Каждый узел может быть либо красным, либо черным
- Корень всегда черный
- Родителем красного узла не может быть красный узел
- Для каждого листового узла количество черных узлов на пути до корня одинаково
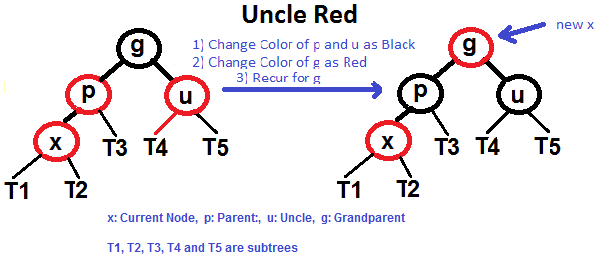
Для обеспечения этих свойств при вставке узла проводится ребалансировка дерева. Сначала пробуем перекрашивание, если оно не работает, то вращение. Если дядя красный, то перекрашиваем, если черный - то вращаем и/или перекрашиваем.
Алгоритм вставки (x - вставляемый узел):
- Делаем x красным и производим стандартную вставку в поисковое бинарное дерево
- Если x - корень, то делаем его черным и завершаем вставку, иначе - красным
- Если родитель x - красный и он корень, то просто делаем его черным и завершаем вставку
-
Если x не корень или родитель x не черный (в этом случае дедушка точно будет черный), то мы получили красный-красный-черный, что нарушает свойство 3. Попробуем это исправить:
- если дядя x - красный, то мы можем просто перекрасить папу и дядю, так как они оба красные и перекрашивание их в черный увеличит количество черных узлов для обоих ветвей деда и не нарушит свойство 4. Однако чтобы не менять количество черных в ветвях нашего поддерева и чтобы не пришлось ребалансировать поддерево брата деда, мы еще и перекрашиваем деда в красный:
- перекрашиваем родителя и дядю в черный
- перекрашиваем деда в красный
-
eсли дяди нет, или дядя х - черный, то мы не можем перекрасить папу в черный, т.к. это увеличит количество черных узлов на одной ветви, оставим неизменным на остальных и автоматически нарушится свойство 4. Поэтому приходится вертеть:
- p - parent узла х, g - grandfather узла х
- возможны 4 случая:
- p слева от g, x слева от p
- p слева от g, x справа от p
- p справа от g, x справа от p
- p справа от g, x слева от p
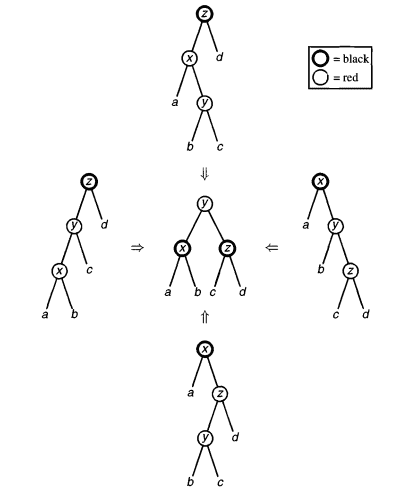
- Для каждого из этих 4 случаев нам нужно нарушающий свойство 3 путь от x вида красный-красный-черный в красный с двумя черными детьми. Как это сделать - смотрим на картинке (картинка из другой книги, поэтому там добавляемый узел - не x, а просто тот, который самый нижний и в кружочке. На этих случаях всегда x < y < z, поэтому y в результате становится корнем поддерева:
- После этого нужно перекрасить наше поддерево, сделав корень черным, а его детей красным.
Вращение дерева:

Декартово дерево
Это тоже сбалансированное дерево поиска, но в нем каждая вершина обладает двумя значениями - ключом и приоритетом. По ключам структура обладает свойствами двоичного поиска, а по приоритета - свойствами кучи. Из-за этого в литературе структуру чатсо называют treap.
Соответствующей теоремой доказывается, что для любого набора ключей и приоритетов есть только один вариант такого дерева. Случайный выбор приоритетов позволит в среднем получить не вырожденное дерево с асимптотикой O(log N).
Поиск в таком дереве осуществляектся за O(log N).
Операции добавления и удаления элементов осуществляются при помощи вспомогательных операций Merge и Split, по O(log N) каждая.
Так же, благодаря операции Merge, такие кучи можно сливать, но только если одно из деревьев строго меньше другого по ключам.
Построить дерево, при определенных ухищрениях, можно за O(N).
В результате получаем:
- обладает почти гарантированно логарифмической высотой относительно количества своих вершин;
- позволяет за логарифмическое время искать любой ключ в дереве, добавлять его и удалять;
- исходный код всех её методов не превышает 20 строк, они легко понимаются и в них крайне сложно ошибиться
- содержит некоторый overhead по памяти, сравнительно с истинно самобалансирующимися деревьями, на хранение приоритетов.
Более подробное описание операций здесь и здесь.
Неявное декартово дерево
При помощи небольшой модификации (а именно, вместо ключа использовать индекс элемента в массиве), получаем возможность использовать следующие операции за время O(log N):
- Вставка элемента в массив в любую позицию
- Удаление произвольного элемента
- Сумма, минимум/максимум на произвольном отрезке, и т.д.
- Прибавление, покраска на отрезке
- Переворот (перестановка элементов в обратном порядке) на отрезке